2025 sous l’angle de l’arithmétique

Carte de vœux du Cabinet

Sans verser dans la numérologie, l’année qui clôt ce premier quart de siècle et ouvre le second est remarquable par son chiffre. En effet, 2025 est le carré de la somme des 9 premiers entiers naturels. Et c'est aussi la somme de leurs cubes.

$\begin{array}{c} 2025 = (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9)^{2} = 1^{3} + 2^{3} + 3^{3} + 4^{3} + 5^{3} + 6^{3} + 7^{3} + 8^{3} + 9^{3} \end{array}$

Que 1+2+3+4+5+6+7+8+9 soit égal à 20 + 25 est une coïncidence. Mais que 2025 soit la somme des 45 (20 + 25) premiers nombres impairs ne l’est pas.

L’explication se trouve dans des identités remarquables.

Pour calculer la somme des entiers de 1 à n, le nombre triangulaire que nous noterons S(n), on connaît l’astuce du jeune Gauss qui consiste à additionner cette somme à elle-même, écrite en sens inverse :
$\begin{array}{l} 1 + 2 + \dots + n \\ n + \dots + 2 + 1 \end{array}$
Le total de chacune des n colonnes ainsi formées étant constant, on en tire $2 n = n (n + 1)$ .
Autrement dit :
$\begin{array}{l} 1 + 2 + \dots + n = n (n + 1) / 2 \end{array}$
La somme des n premiers nombres impairs forme le carré de n.
Cela est vrai pour le carré unité : $1^{2} = 1$ .
Et selon la formule bien connue $(n + 1)^{2} = n^{2} + (2 n + 1)$ , pour passer d’un carré de côté n à un carré de côté n+1, il faut lui rajouter 2n+1 carrés unités (n en colonne, n en ligne et 1 en diagonale), ce qui représente la valeur du n+1 ^ième nombre impair.
Par récurrence :
$\begin{array}{l} n^{2} = 1 + 3 + 5 + > \dots + (2 n - 1) \end{array}$

La figure ci-contre visualise la décomposition d’un carré de côté 45 en 45 équerres symétriques imbriquées, toutes de longueur impaire.
Lorsqu’on passe du carré de la somme S(n–1) à celui de la somme S(n) des entiers de 1 à n, l’accroissement est de n³.
Selon notre premier point en effet, cet accroissement vaut le quart de la différence :
$\begin{array}{l} (n (n + 1))^{2} - ((n - 1) n)^{2} = n^{2} ((n + 1)^{2} - (n - 1)^{2}) = n^{2} (4 n) = 4 n^{3} \end{array}$
Partant de 1 = 1² = 1³, il en résulte :
$\begin{array}{l} (1 + 2 + 3 + \dots + n)^{2} = 1^{3} + 2^{3} + 3^{3} + \dots + n^{3} \end{array}$
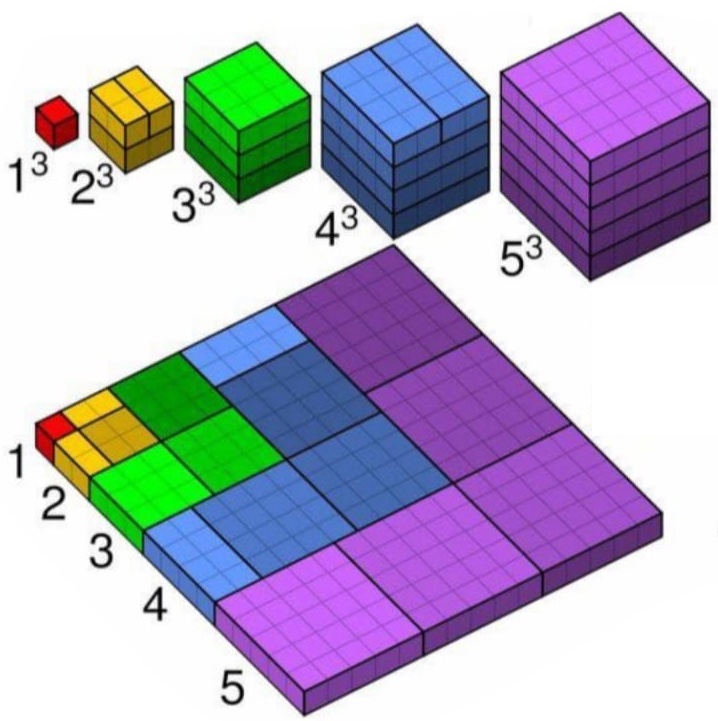
La figure ci-contre montre comment construire géométriquement ces cubes à partir du découpage d'un carré de ce type. Ici, S(5) = 15.
Vu comme la différence de deux carrés de côtés S(n) et S(n–1), le cube n³ est d’après notre second point une somme de nombres impairs consécutifs.
Sachant que :
- la suite des S(n–1) premiers nombres impairs dont la somme est S(n–1)² s'arrête à la valeur $2 S (n - 1) - 1 = n (n - 1) - 1$
- la suite des S(n) premiers nombres impairs dont la somme est S(n)² s'arrête à la valeur $2 S (n) - 1 = n (n + 1) - 1$
n³ est précisément la somme des n nombres impairs compris entre n(n-1)+1 et n(n+1)-1.

Ce résultat est attribué au mathématicien grec Nicomaque de Gérase, « inventeur de la musique », qui écrivit dans son Introduction à l’Arithmétique au second siècle de notre ère :

« Tous les nombres formés d'un même nombre pris trois fois comme facteur, c’est-à-dire les cubes, […] sont l'œuvre des impairs […]. En effet, les nombres impairs depuis l'unité jusqu'à l'infini étant exposés en rang, faites l'observation suivante : le premier forme le cube virtuel; les deux suivants ajoutés ensemble forment le second cube; les trois suivants forment le 3e ; les quatre d'après, le 4e ; les cinq à la suite, le 5e ; les 6 à la suite, le 6e ; et ainsi à l'infini. »

(Livre second, chapitre 20, traduit du grec par Henri Martin)

Résumons :

$\begin{array}{rcl} S (n) = \sum_{i = 1}^{n} i = n (n + 1) / 2 (1) \\ n^{2} = \sum_{i = 1}^{n} (2 i - 1) (2) \\ {(\sum_{i = 1}^{n} i)}^{2} = \sum_{i = 1}^{n} i^{3} (3) \\ n^{3} = \sum_{i = S (n - 1) + 1}^{S (n)} (2 i - 1) (4) \end{array}$

Pour en revenir à notre cas particulier :

        2025 = (1 + 2 + 3 + ... + 9)² 
             = 1³ + 2³ + 3³ + ... + 9³
             = 1 
               +3+5
               +7+9+11
               +13+15+17+19
               +21+23+25+27+29
               +31+33+35+37+39+41
               +43+45+47+49+51+53+55
               +57+59+61+63+65+67+69+71
               +73+75+77+79+81+83+85+87+89

Bonne année !

> Clip publicitaire Implexe